If we want to combine both mutations of the concept tube to get a bent tube that narrows in the middle, we need to change tactics, and this is where pointsandfaces can show it’s advantages by using the functions in pointsforge.scad.
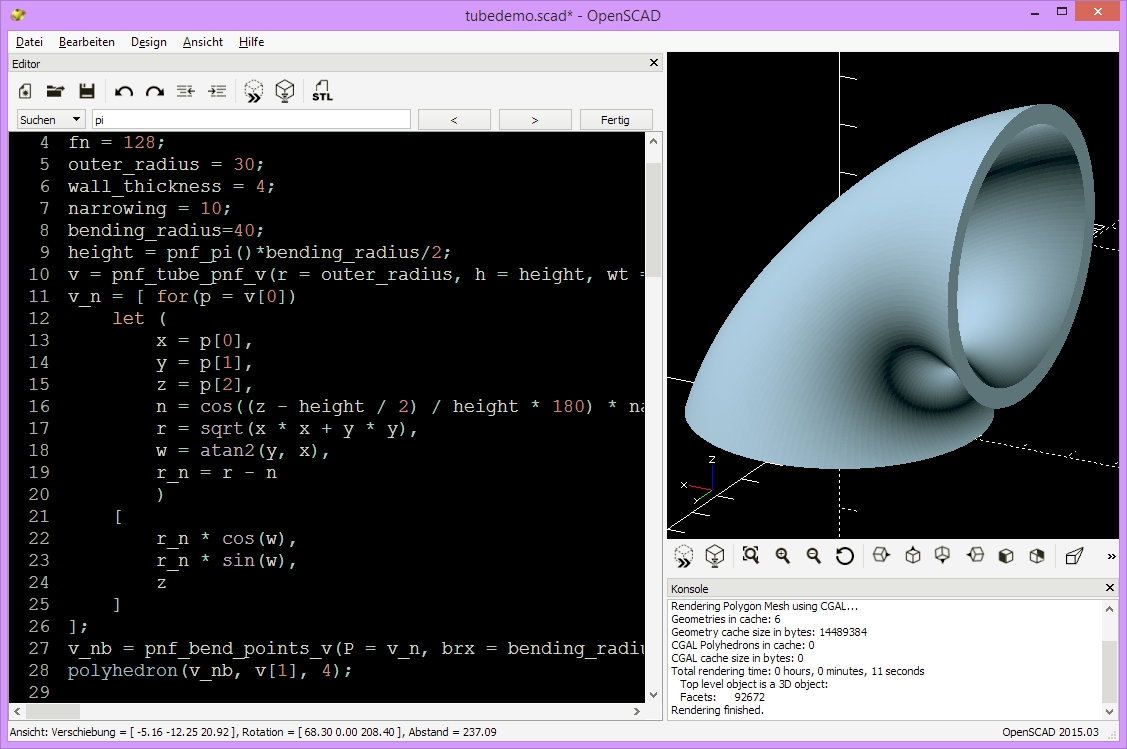
As you can see, the listing is a bit more complicated then the previous examples, but let’s take a closer look to demystify this.
use <inc/pnf/pnf_cylinder.scad>
use <inc/pnf/pnf_littlehelpers.scad>
use <inc/pnf/pnf_pointsforge.scad>
fn = 128;
outer_radius = 30;
wall_thickness = 4;
narrowing = 10;
bending_radius=40;
height = pnf_pi()*bending_radius/2;
v = pnf_tube_pnf_v(r = outer_radius, h = height, wt = wall_thickness, nz = 180, fn = fn);
v_n = [ for(p = v[0])
let (
x = p[0],
y = p[1],
z = p[2],
n = cos((z - height / 2) / height * 180) * narrowing,
r = sqrt(x * x + y * y),
w = atan2(y, x),
r_n = r - n
)
[
r_n * cos(w),
r_n * sin(w),
z
]
];
v_nb = pnf_bend_points_v(P = v_n, brx = bending_radius);
polyhedron(v_nb, v[1], 4);
The first difference that we recognize when we read the listing from top to bottom is the including of pnf_pointsforge.scad and pnf_littlehelpers.scad. The incude file pnf_pointsforge.scad gives us functions to modify the positions of points depending on their positions, which enables us to “forge” our objects. The iron is the points and we want to swage, bend and twist this iron to get the desired shape. And we don’t use a hammer but functions. Like a smith we have ready-to-use tools in our smithy and special tools that we make for one or a few pieces.
In this example we use both, a tool in our smithy, which is called bend_points_v() to bend our tube and we make our own tool to narrow our tube. Narrowing is applied first. The narrowing is dependent on the height, it is highest in the middle, and to have a smooth narrowing, we use the sin() function to calculate it. To apply the calculated narrowing to the points is not as easy as creating the polygon to rotate_extrude(). We don’t have a simple input-parameter but a combination of 3, the x,y and z-positions of each point. So it requires a bit of trigonometry to calculate the new positions. Whenever it gets a bit complicated, I like to split the problem into litte parts, which in this case is the use of intermediate variables within the let()-statement. In order to make the code more readable, we first extract the positions from the point:
x = p[0],
y = p[1],
z = p[2],
Then we want to know the point’s distance from the middle of the tube, which in our example will be 30 for outer points and 26 for inner points. But the distance is not in the given array, so we calculate it using Pythagoras:
r = sqrt(x * x + y * y),
We also need to know the angle of the point in relation to the middle, where the atan2()-function helps us to avoid the special cases that have to do with division by zero:
w = atan2(y, x),
Now we have a distance and an angle. All we have to do now is to calculate the respective narrowing by using the z-position and subtracting this narrowing from the distance,
n = cos((z - height / 2) / height * 180) * narrowing,
r_n = r - n
and recalculate the position with sin() and cos(), which is so simple, that we do it outside the let()-statement and inside the result definition:
[
r_n * cos(w),
r_n * sin(w),
z
]
But we are not finished, yet. The array is not yet bent. This is Simple, because we can use a tool in our smithy, the function bend_points_v(), which does, what its name says. It would go beyond the scope of explaining this example, to go into the internals of bend_points_v(), so we only have a quick glance at it, before we go further into depth:
function bend_points_v(P, brx = 0, bry = 0) =
[
for (p=P)
let
(
x = p[0],
y = p[1],
z = p[2],
wx = brx ? (z / (brx * 2 * pi()) * 360) : 0,
wy = bry ? (z / (bry * 2 * pi()) * 360) : 0,
x2 = x * cos(wx),
y2 = y * cos(wy),
z2 = x * sin(wx) + y * sin(wy)
)
[
brx ? (-brx + (cos(wx) * brx) + x2) : x,
bry ? (-bry + (cos(wy) * bry) + y2) : y,
sin(wx) * brx + sin(wy) * bry + z2
]
];
Actually it’s simple. We have two bending directions, x and y. Let’s look at one of them, say x. Bending is done by rotating each point round the middle axis of the bending for an angle, that depends on the height (z-value) of that point. The new position is calculated with trigonometry.
But how does the function tube_pnf_v() work and why do we want to know this?
Let’s have a look at some internals.