This example mainly introduces the function screw_extrude_pnf_v(). This function’s main purpose is to make threads, but it can be used for more than ISO-Threads. A thread seems to have a complex geometry, and I admit that calculating the coordinates of the points of a thread is not as easy as calculating the points of a cylinder, but calculating the faces is almost the same as for a cylinder or any other object, that can be divided into rows of pairs of triangles surrounding it. Now think of the thread as a long profile coiled around a imaginary cylinder. From the faces’ point of view it doesn’t matter, whether the underlying points form a shape that goes straight up or is coiling around.
In pnf_screw_extrude_pnf_v() the profile of the thread (for example a triangle in normal ISO-threads or the silhouette of a person in some piece of art) is assigned by the first parameter as an array of points in two dimensions (x,y), and again it is a question of trigonometry to calculate the positions of the points of a coiling extrusion of this polygon.
There is one problem that makes the difference, i.e. we have two ends, that somehow have to be closed without any counter-side that can be connected to. In the example with the tube we circumvented this problem by going back to the beginning, but here we can’t. There are two solutions for this problem, and both have their right to exist:
1. Triangulation
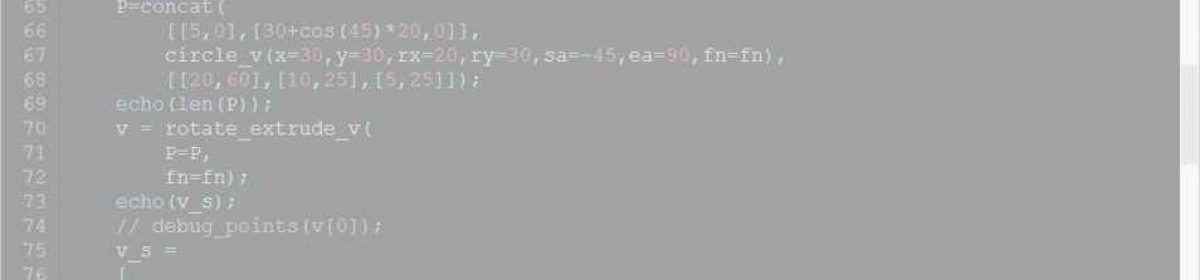
Triangulation turns a polygon into a set of triangles so it can be used as the surface of one or more faces of an object.
2. Thinning out
The elegant solution would be a triangulation of the polygon and a kind of lid and floor consisting of the points and faces of the triangles. But how can we triangulate any polygon to get a valid ending on both sides?
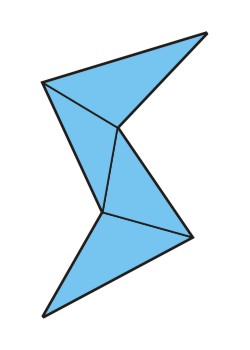
An intermediate solution would be, to introduce a further parameter with the points and faces data that the user of the function would have to determine manually, but this is also not yet implemented. Why? Because it wasn’t yet necessary for me. All the threads I have yet implemented, have a soft start and ending and don’t require a flat surface in shape of the profile at start and end. To see why this makes a complex triangulation unnecessary, let’s try different tactics for triangulation. The most obvious tactic is to chose one of the points of the polygon as a center point all the other points have triangles going to. Another tactic would be to chose one middle point and connect all the other points with triangles.
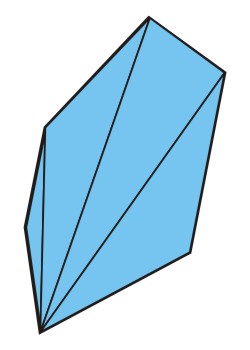
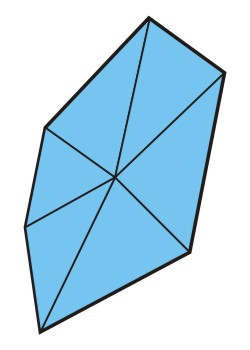
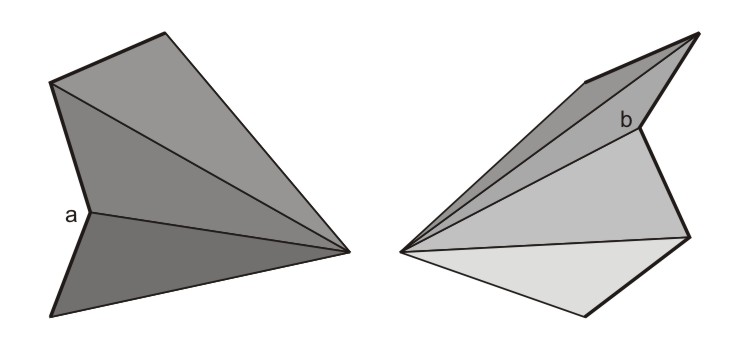
But neither work for any shape. What if there is an angle pointing to the inside?
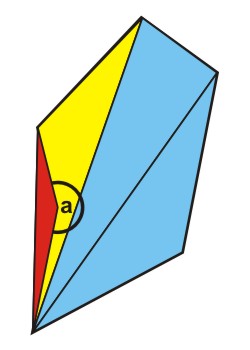
For the tactic of choosing one of the points it would be a disaster. The red triangle would be outside the polygon and furthermore it would be inside out. leaving it away would not be sufficient, because the yellow triangle still leaves the polygon. In this case, it would be sufficient, to choose the point with the inside angle (a) as the center point.
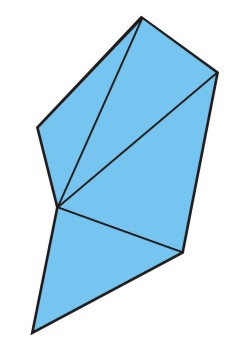
But what if there are two angles pointing inside? There are cases where it would still be sufficient to chose the right point, but there are also other cases, where there is no way to chose one point to connect the other points to.
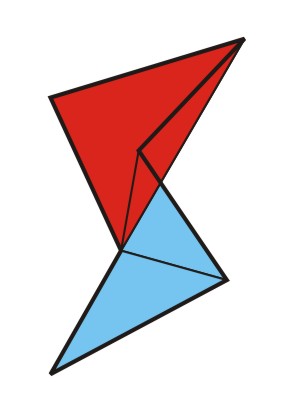
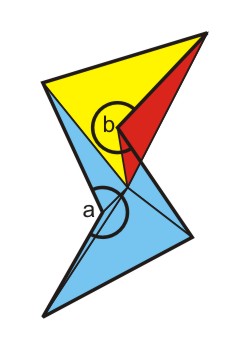
But what if we go into the third dimension? What if the middle point lies above the plane on which the polygon resides? As this webpage is a two-dimensional medium, I have to show you from two sides. Below you see two views of the example above with a middle point shifted into the third dimension.
There is a function in pointsandfaces.scad, that connects one point to multiple others. It’s called concentric_faces_v() and it is very simple, but useful:
function concentric_faces_v(n,center,first,close=false) =
[
for (i=[0:1:n-1])
[
center,
first+i,
first + (((i < n - 1) || (!close)) ? i + 1 : 0)
]
];
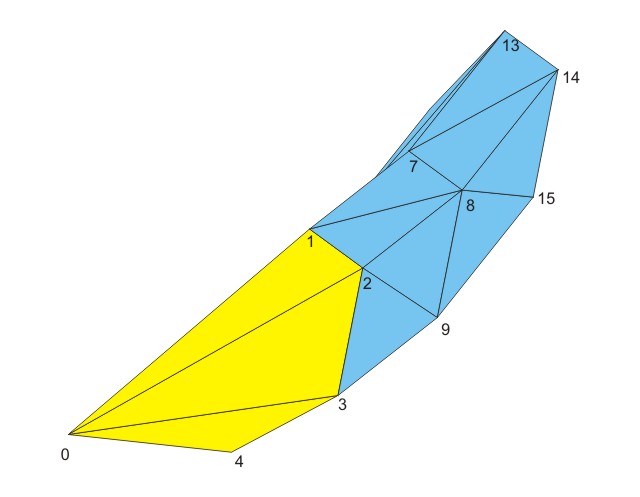
Note, that the order of the points determines, which is the inside and which is the outside of the object. For the start of the thread it should be all right. Our polygon has 6 edges, so the first parameter “n” is 6. The middle point of the start has the index 0, so the second parameter “center” is 0. The first point of the first ring is indexed by 1, so the third parameter “first” is set to 1 and “close” ist set to true, of course. For these values concentric_faces_v() returns the following 6 faces:
[[0, 1, 2], [0, 2, 3], [0, 3, 4], [0, 4, 5], [0, 5, 6], [0, 6, 1]].
The first face, which is [0, 1, 2], looks all right, the second and third, too. We cant see the other 3, but we can imagine them, and also the last (closing) face looks all right, [0, 6, 1] also defines the faces’ points in clockwise order, so the start of the thread looks all right.
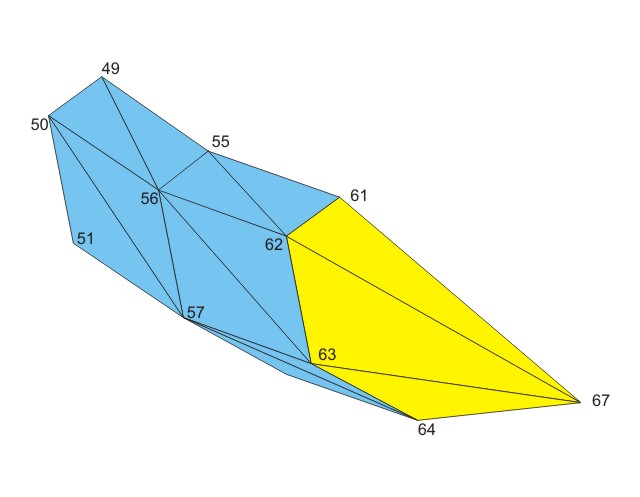
This is different with the ending of the thread. In this example the center point has the index 67, and the last ring before the end starts with 61. With these values concentric_faces_v() returns the following 6 faces:
[[67, 61, 62], [67, 62, 63], [67, 63, 64], [67, 64, 65], [67, 65, 66], [67, 66, 61]]
We can see immediately, that the points go anti-clockwise, and this is not what we want. We could change the function concentric_faces_v() to give it an additional parameter telling the index-difference between two points and set it to -1 or we can just flip the returned faces with turn_sides_faces_v(), which returns
[[62, 61, 67], [63, 62, 67], [64, 63, 67], [65, 64, 67], [66, 65, 67], [61, 66, 67]].
And this suits our needs. [62, 61, 67] goes clockwise, so do the other faces.
The middle point is also the end of the thread. In screw_extrude_pnf_v() the middle point is positioned in the center of the coordinate system of the polygon, thus if you place a thread on a cylinder, the polygon should be designed in a way that the side that touches the cylinder is positioned exactly on the y-axis and the little Overlap to avoid non-“watertight” objects is given by adding a very small value to the radius(es).
It requires only little additional calculation for the positions of the points to use this to implement soft thread-ends, because the polygon-data only has to be scaled at the beginning and end in a way, that can be defined by parameters. And there are quite a few parameters, because using this function in different situations I had the necessity to make it more flexibel. But let’s keep it simple, first:
use <inc/pnf/screwextrude.scad>
tol = 2;
fn = 256;
p = 30;
ScrewExtrude
(
P=[[0,p/2-tol],[p,p/2-tol],[p,-p/2+tol],[0,-p/2+tol]],
r=100, p=p, d=720, sr=90, erxy=90, erz=0, fn=fn, rf="sin"
);
In this case we use the wrapper module ScrewExtrude(), because unless you are Dali, you will probably not want to bend or forge threads and seldom use the function screw_extrude_pnf_v().
The Result is this:

What catches the eye here is the different shapes of the both endings of this coil. This can be controlled with the “starting ramp” and “ending ramp” parameters sr, er, srxy, erxy, srz and erz. The lengths of the ramps can be different for the x/y-direction and the z-direction. The sr.. parameters tell the length of the respective ramp in degrees. We have 4 ramp dimensions:
| ramp | dimension | length-parameter | form-parameter |
| start | x/y | srxy | srfxy |
| start | z | srz | srfz |
| end | x/y | erxy | erfxy |
| end | z | erz | erfz |
The parameter sr is the default for srxy and srz, er is the default for erxy and erz.
This all doesn’t mean, that triangulation of polygons is not to be implemented in future. Actually, besides writing this documentation, taking care of house and daughter, I am currently experimenting with it, because I want to implement a linear_extrude_pnf_v() function, and it would also be a nice option for rotate_extrude_pnf_v(), to have flat endings, if desired.